Now, we want to parameterize the policy $\pi(a|s,\Theta) = Pr(A_t=a|S_t=s,\Theta_t=\Theta$ as long as it is differentiable. To find the best policy, we want to optimize according to $J$ using gradient ascent.
$$ \Theta_{t+1} = \Theta + \alpha \nabla J(\Theta_t) $$
Discrete action: Soft-max policy
We compute preference $h(s,a,\Theta) = \Theta^T x(s,a)$. One of the most common way to parameterize policy is soft-max:
$$ \pi (a|s,\Theta) = \frac{e^{h(s,a,\Theta)}}{\sum_b e^{h(s,b,\Theta)}} $$
One advantage of soft max parameterization is that it can make the optimal determinstic policy.
The second advantage is that it enables the selection with arbitrary probabilities.
If policy is a simpler function to approximate, it is faster to use it than action-valution functions.
The Policy Gradient Thereom
What is the objective of policy gradient?
We define the performance measure as $J(\Theta) = v_{\pi_{\Theta}}(s_0)$
Actually, this is the expected return.
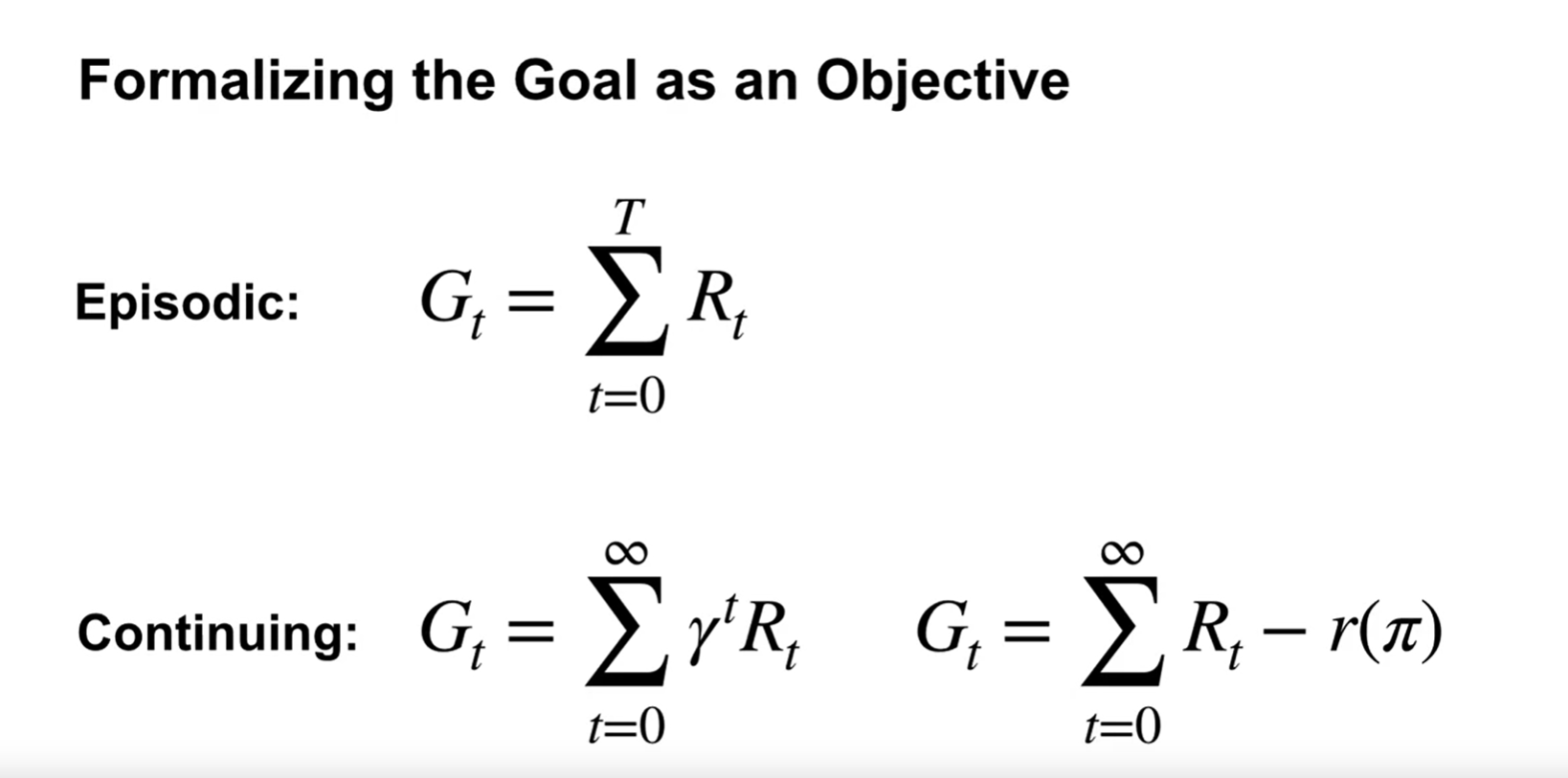
If we define the objective as the average reward $r(\pi)$, we can unroll it as the following:
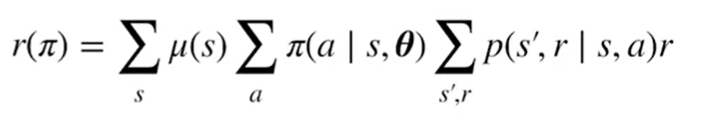
Therefore, the gradient is
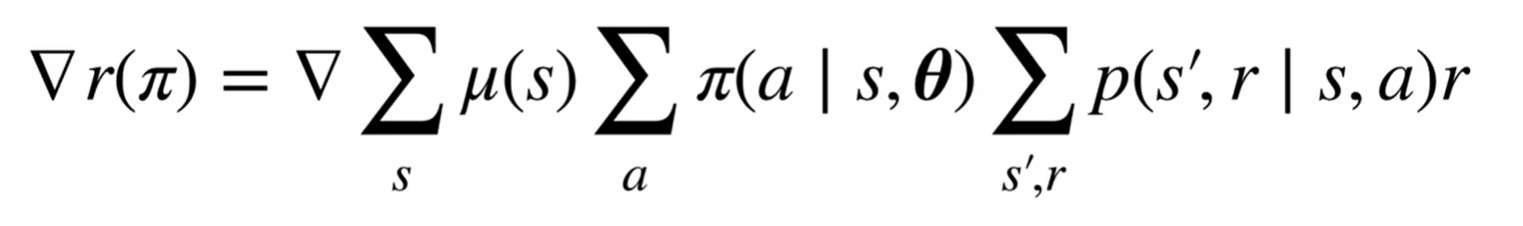
After derivation, according to the theorem:
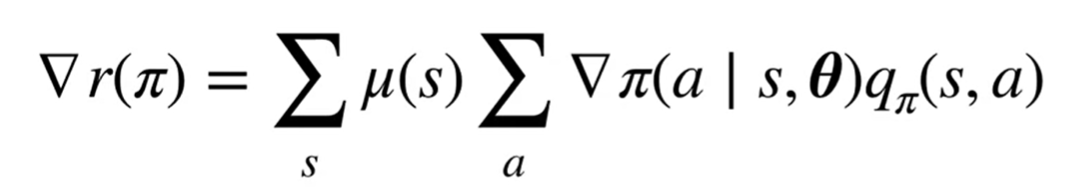
To transform it into a stochastic gradient ascent step:
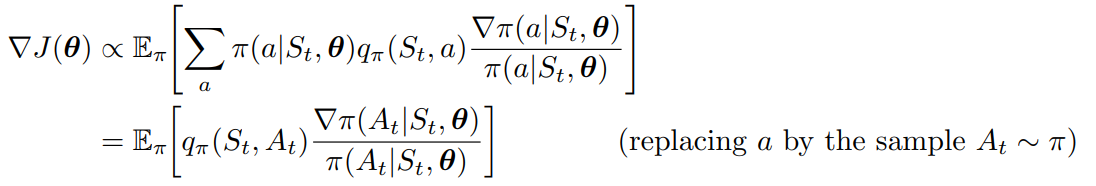
We can have the update rule as:
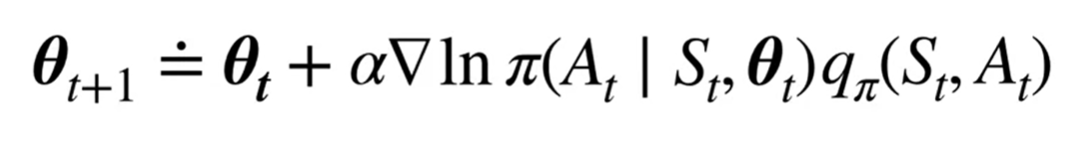
Actor-Critic
Now we have a parameterized actor to perform and improve policy.But how to compute value function? We use another function approximator to estimate $q$ (or $v$), as a critic.
For Average Reward Semi-Gradient TD(0)
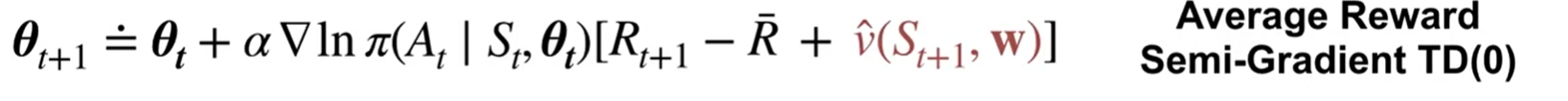
after adding a baseline:
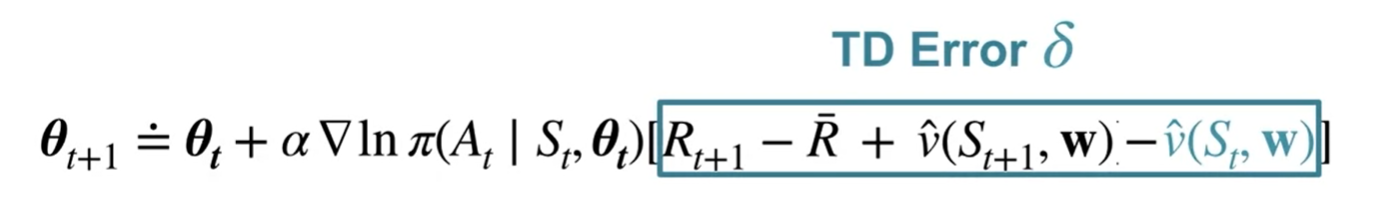
We can prove that the baseline does not affect! Adavantage is it reduces update variance.

For Discounted Return Semi-Gradient TD(0)
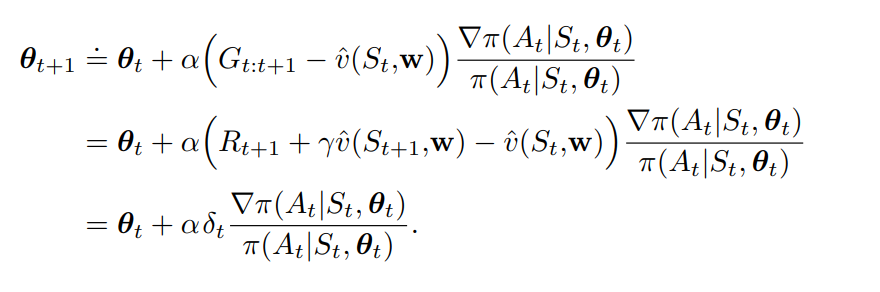

Continuous action: Gaussian Policies
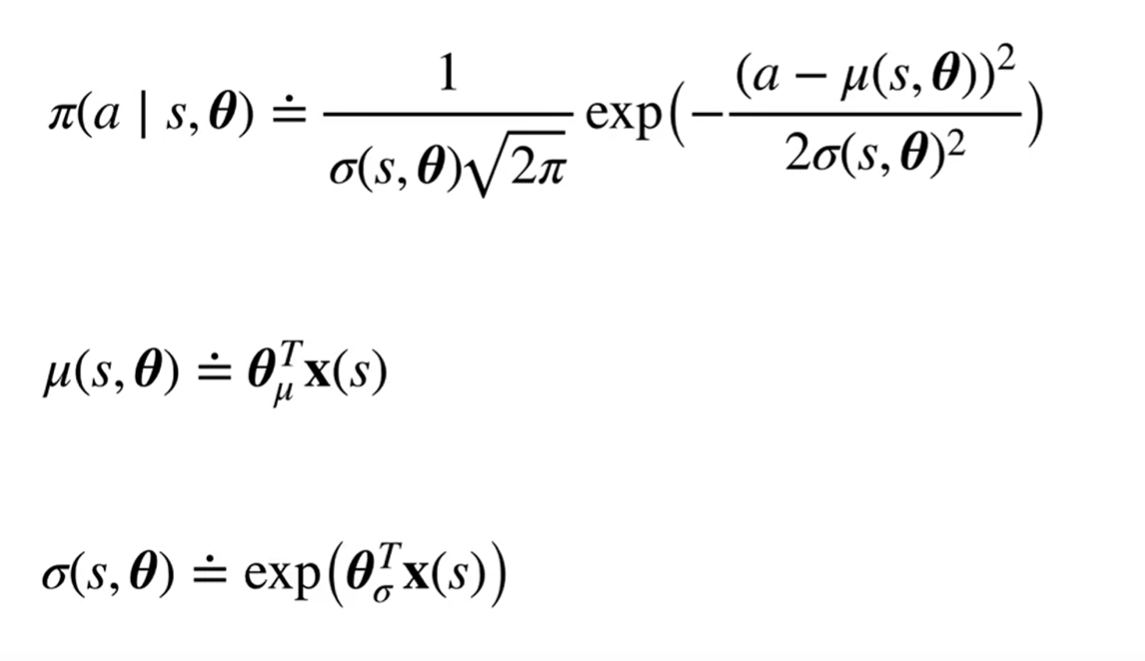
Measure how RL agents perform
exponentially weighted average reward