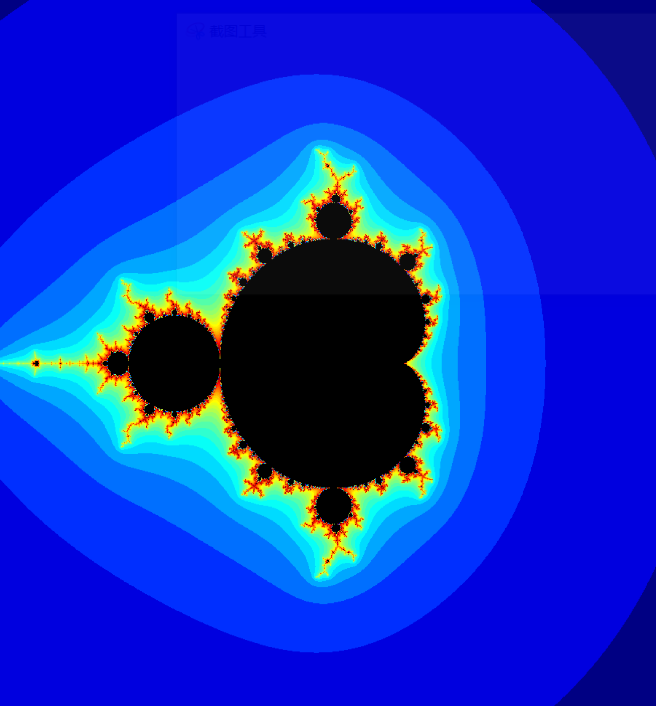
- 空间上的分形和时间上的混沌有相似性。一个动力方程是时间上的混沌,会收敛到吸引子,根据此画出的动力平面和参数平面是空间上的分形。
Mandelbrot Set
复迭代
有一个关于z的复映射with 参数c如下:
$$f_c(z) = z^2 +c$$
我们想要知道在参数平面中临界点$z = 0$的轨迹是否有界,即
对于一个c,根据迭代规则
$$z_{n+1} = z_{n}^2 + c$$
生成的序列${x_0,x_1,…} -> \infty$,则无界,$c \notin M,$ 如果序列有界,则$c \in M$。
另外我们还想要知道在动力平面中$c \in C$, 不同z0 的值产生的轨迹是否有界,此时$z_0 \in Julia,$ 如果序列有界,$z_0 \notin Julia$ 如果序列无界。
Algorithm 逃逸时间算法
为了绘制参数平面中的M集,我们需要确定每个c是否属于M集,这里用到了逃逸时间算法。
逃逸准则
对于一个复数$z_n = x_n +iy_n$, 模$|z_n| = \sqrt {x_n^2 + y_n^2}$。我们claim:
如果对于一个复数序列 ${z1,z2…zn}$ 有$|z_j| > max(2,|c|)$则序列将逃逸到无穷大。
证明
当 $|z_j| > max(2,|c|)$, 则
由$|z_j|>2$ 可知 $|z_j| = 2+e,$ for $e\in \R^+$
$|z_j^2| = |z_j^2 +c-c| \geq |z_j^2+c| + |c|$
因此,我们得到
$|z_{j+1}|=|z_j^2 + c| \geq |z_J^2|-|c| = |z_j|^2 -|c| > |z_J|^2-|z_j| > |z_j|(|z_j|-1) > |z_j|(1+e)$
那么在k次迭代后,我们得到
$|z_{j+k}^2 + c|> |z_j|(1+e)^k$
序列趋于无穷
如果$|c|\geq2$ ,可得
$z_0 = 0, z_1 = c$, $z_2 = c*(c+1)$,
$|z2|/|z1| = |c^2+c|/|c| >1$ 因为 $|c+1|>1,|c^2+c|>|c|$
那么对于任意$z_j$, 假设$|z_j| = p > 1$, 我们有$|z_{j+1}|/|z_j| > e$,对于$e > 1$
那么根据数学归纳法,我们知道序列趋于无穷。
z需要判断大于2来证明这是个无界序列吗?不用。
逃逸时间算法
对于每个复参数平面上的点c,我们生成一个序列$Z$,怎么判断这个序列是否有界呢?根据逃逸准则,我们规定在${z1…zn}$里,如果$|zj| < R$,判断有界,但其实也有可能这个序列是无界的,反之,这个序列无界。所以我们需要确定以下超参数:
- 复平面范围$C = {c=x+iy;x1 \leq x \leq x2, y1\leq y\leq y2}$
- 分辨率$gridSize$
- 逃逸半径$R = max(2,|c|)$
- 逃逸时间$N$=最大迭代次数
如果R小于2或$|c|$,则一些真正有界的会被判断为无界;因此R要设置为大于2。
为了观察结构,我们也可以设置在不同n逃逸出去的c值画不同颜色,那么就需要一个变量记录这一特点,代码中为count,每一个iteration对z值的判断,如果逃逸则累加1,如果没有逃逸则累加0,结果是对于每个c值,z越早逃逸count数值越大,后期绘图log化后可以map到不同颜色上。
我们可以确定算法结构:
set N, gridSize, C, R
initial z = 0, c in C
% 批量计算
for i = 1 to N:
z = z**2 + c
count = count + (|z| <= R)
end for
count = log(count)
% 画图
MATLAB Implementation
% Set up
N = 500; % max iterations 最大迭代次数(逃逸时间)
gridSize = 1000; % resolution 分辨率
R = 2 % 逃逸半径
% C 复平面确定
xlim = [-2, 2]; % x 范围
ylim = [-2, 2]; % y 范围
t = tic();
x = linspace( xlim(1), xlim(2), gridSize );
y = linspace( ylim(1), ylim(2), gridSize );
[xGrid,yGrid] = meshgrid( x, y );
% Initialization
c = xGrid + 1i*yGrid;
count = ones( size(z0) );
z = 0; % 临界点
% Calculate
for n = 0:N
z = z.*z + c;
inside = abs( z )<=R; % 逃逸准则判断
count = count + inside;
end
count = log( count );
% Show 画图
cpuTime = toc( t );
fig = gcf;
fig.Position = [200 200 600 600];
imagesc( x, y, count );
colormap( [jet();flipud( jet() );0 0 0] );
axis off
title( sprintf( '%1.2fsecs (without CPU)', cpuTime ) );
实验结果观察
R = 2
R = 1000
$$z = z^4 +c$$
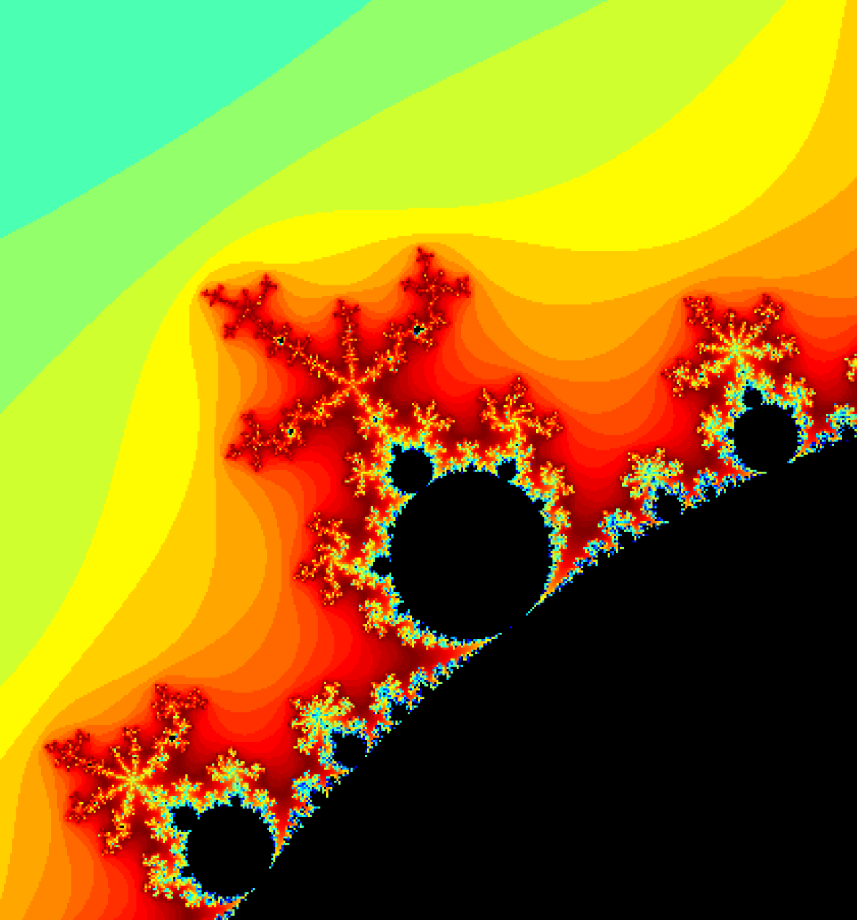
增大gridSize分辨率观察自相似性
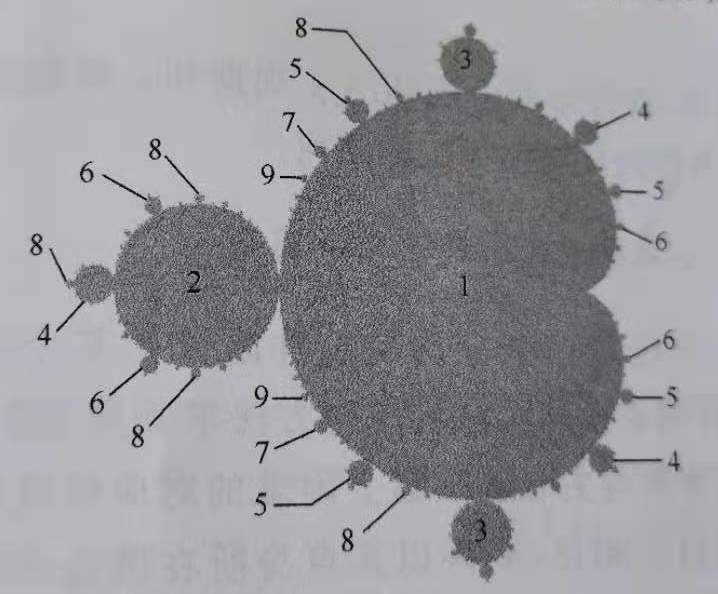
Mandelbrot set 稳定周期
- 大心脏内的c产生的序列收敛到1个accumulation point,这个圆盘是个1-周期圆盘!
- 其他!
tips
为了让导出的图片高清一点,在导出界面找到“导出设置”,并修改“渲染”-“分辨率”为600,导出为tif文件